Introduction to Fuzzy Logic

What is Fuzzy Logic?

Fuzzy logic is a form of many-valued logic that deals with approximate, rather than fixed and exact reasoning. Compared to traditional binary sets (where variables may only be true or false), fuzzy logic variables may have a truth value that ranges between 0 and 1. This concept was introduced by Dr. Lotfi Zadeh in the 1960s as a way to process the uncertainty inherent in many problems. It is built on the foundation of fuzzy set theory. In fuzzy set theory, each element’s membership of a set is expressed with a value between 0 and 1, representing its degree of truth. This allows for a more nuanced approach to reasoning, especially in cases where the binary distinction between true and false does not adequately describe reality.

Linguistic Variable

A linguistic variable is a variable whose values are words or sentences, rather than numbers. In game development, this could be something like an enemy’s threat level, which might be defined as “low,” “medium,” or “high.” Linguistic variables allow game developers to describe complex behaviors or states in a way that’s intuitive and closely mirrors natural language, making it easier to conceptualize and implement nuanced game logic.

Fuzzy Set

A fuzzy set is a collection of objects with a continuum of grades of membership. Unlike traditional sets, where an object either is or isn’t a member of the set, objects in a fuzzy set have a degree of membership ranging between 0 (not a member) and 1 (full member). For example, in a game, the concept of “nearby enemies” can be represented as a fuzzy set, where enemies are not simply classified as “nearby” or “not nearby” but have varying degrees of “nearbiness” based on their distance from the player.

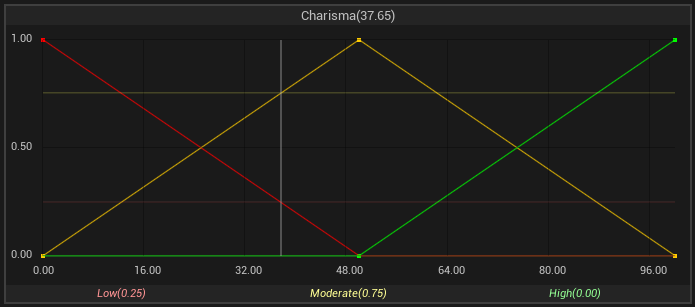
In the image above, you will find an example of how the linguistic variable Charisma is defined, along with its associated fuzzy sets: Low, Moderate, and High. The low charisma category is characterized by a Linear Z-Shaped membership function, peaking at a crisp value of 0.0 and linearly declining to no membership at crisp value 50.0. For moderate charisma, a Trapezoidal membership function is used, with its peak at 50.0. Membership decreases to zero at the crisp values of 0.0 and 100.0. The high charisma category employs a Linear S-Shaped membership function, where membership begins at no membership at a crisp value of 50.0 and peaks at 100.0. Given these definitions, a Charisma score of 37.65 translates to membership values of 0.25 for Low, 0.75 for Moderate, and 0.0 for High.

Evaluating a Fuzzy Logic System

A fuzzy logic system operates through a series of distinct phases to process input and generate output.

flowchart LR
  subgraph fls[Fuzzy Logic System]
    direction LR
    fzf[Fuzzification] --fuzzy value-->fis[Inference] --fuzzy value-->dfz[Defuzzification]
  end
  in[Crisp Input] -->fzf
  dfz -->out[Crisp Output]

To better illustrate the phases of a fuzzy logic system, let’s examine a specific example. The system’s setup is depicted in the image below:

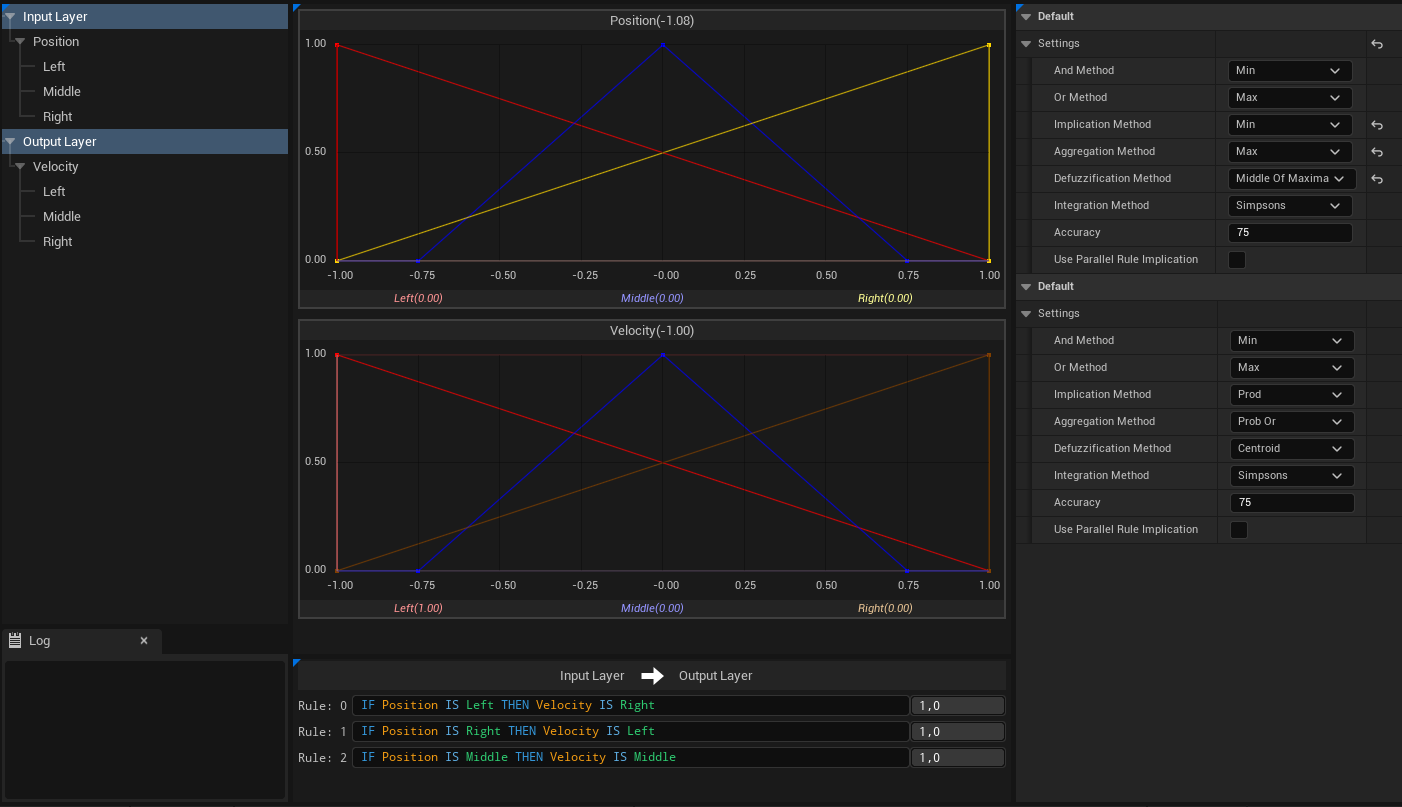
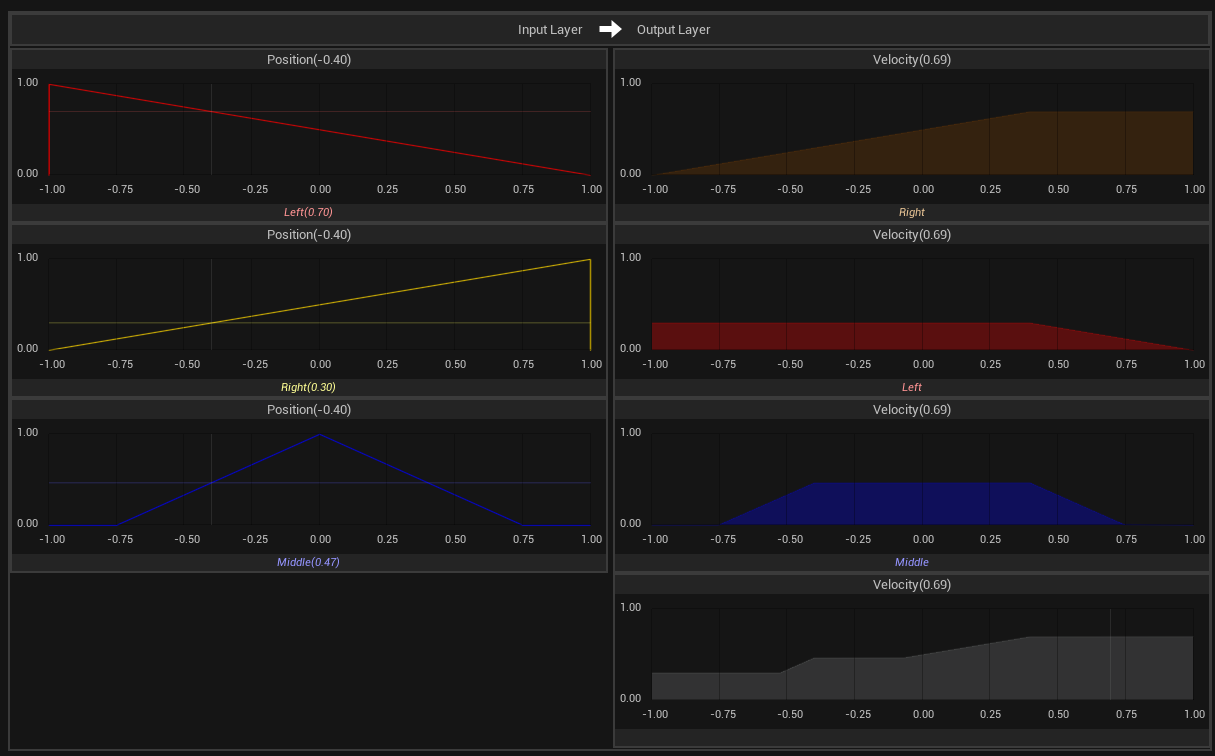
This system is designed to control an agent tasked with avoiding obstacles approaching from both the left and right sides. It utilizes two linguistic variables: Position, which represents the nearest obstacle’s position relative to the agent as an input, and Velocity, which indicates the desired movement direction to dodge the obstacle, as an output. The range for these linguistic variables are defined from -1 (left) to +1 (right). Each linguistic variable is categorized into three fuzzy sets: Left, Middle, and Right, with their definitions visible in the graph views in the center of the image. Settings for the system are outlined in the right-hand panel. Below the image, three fundamental rules that govern the system are presented. These rules are pretty straightforward and simple.

1) Fuzzification

Initially, fuzzification converts crisp numerical inputs into fuzzy values based on predefined linguistic variables and membership functions. This phase is basically a function evaluation. The crisp value for each input linguistic variable is supplied as the input parameter for the membership functions associated with each fuzzy set. The outcome of this membership function evaluation states the degree of truth, also known as the membership value.

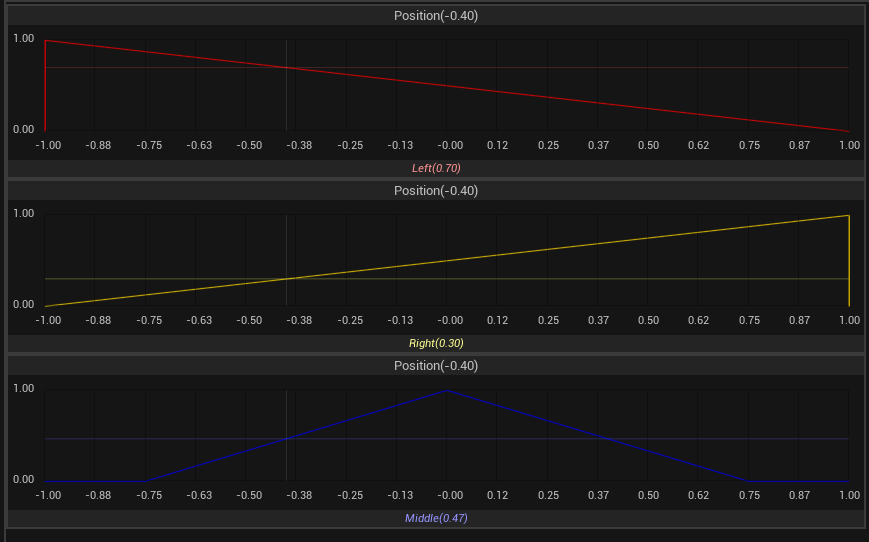
In the image above, the input value of -0.40 is provided for the Position variable. Once this crisp value undergoes fuzzification, the resulting membership values for the fuzzy sets are calculated to be 0.70 for Left, 0.30 for Right, and 0.47 for Middle.

Ideally, the sum of the membership values at any given point should total 1.0. However, with the Fuzzy Logic Designer plugin, adjustments can be made to achieve results that better align with your specific objectives.

2) Inference

Following this, the inference engine applies a set of fuzzy rules to the fuzzified inputs. These rules, crafted to mimic human reasoning, evaluate the inputs’ implications and determine the appropriate fuzzy outputs. The process of aggregation then combines the outputs from multiple rules into a single fuzzy set, ensuring a cohesive response to the inputs.

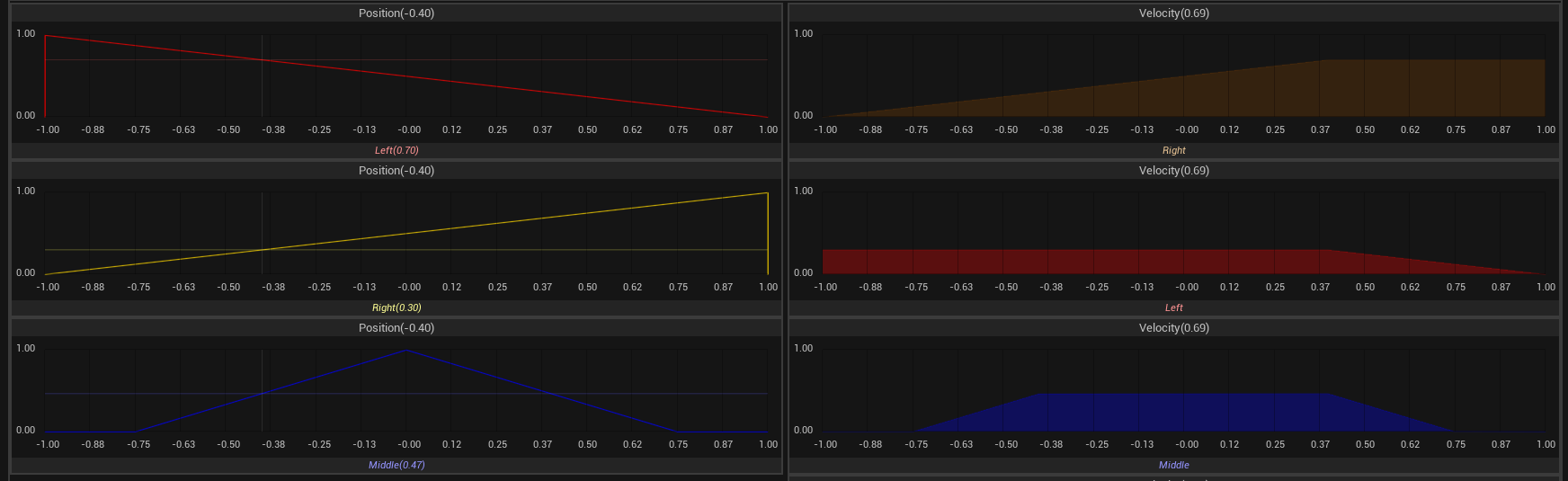
In the image above, an implication process is depicted. The result of this process can differ based on the chosen implication method. For this instance, the implication method is set to the Minimum method. This phase is crucial for the actual reasoning between input and output. The minimum method for implication can be visualized as dividing the membership function of the consequent (output) linguistic variable in half with a horizontal line. This line is drawn at the membership value of the antecedent (input) linguistic variable, highlighting the area beneath it. This visualization represents the initial step in the reasoning process and is repeated for each rule within the system.

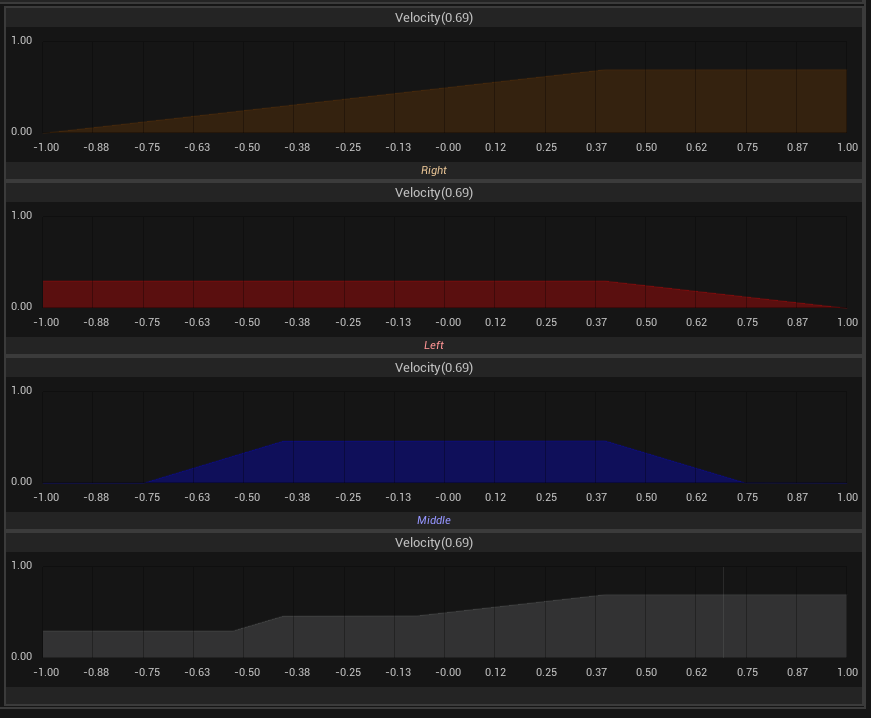
In the image above, the aggregation process is illustrated. The outcome of this process varies depending on the selected aggregation method. In this case, the aggregation method is the Maximum method. This method combines the shapes generated during the implication phase—where the membership function was split and the area beneath highlighted—into a single composite without smoothing. Essentially, it merges all the modified membership functions provided by the implication phase into one unified membership function. This combined function then represents the maximum value across all included membership functions.

3) Defuzzification

Finally, defuzzification translates this fuzzy output back into a crisp value, providing a concrete action or decision.

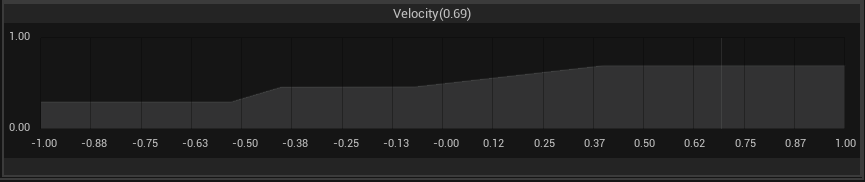
The image provided shows the defuzzification process for our example. The specific outcome of this process is influenced by the choice of defuzzification method, integration method, and the level of accuracy employed. In the settings of this example, the defuzzification method is defined as the Middle of Maxima method. This method operates by identifying the maximum value(s) across the aggregated membership function that resulted from the aggregation process. If there is a single maximum, this method takes this value as the output. In cases where multiple maxima are present, it calculates the midpoint between the first and last maxima, effectively averaging the peak values.

After completing all phases of the fuzzy logic system evaluation, a crisp input value for Position of -0.40 resulted in a Velocity output of 0.69. Given that the left side is denoted by negative values and the right side by positive values, we can conclude that our system successfully made a decision to move the agent towards the right side in response to an obstacle on the left side.